Trong bài này, ta sẽ tập trung vào ví dụ cơ bản về triển khai hồi quy tuyến tính bằng cách sử dụng TensorFlow. Hồi quy logistic hoặc hồi quy tuyến tính là một cách tiếp cận máy học có giám sát để phân loại các danh mục rời rạc theo thứ tự. Mục tiêu của trong bài này là xây dựng một mô hình mà qua đó người dùng có thể dự đoán mối quan hệ giữa các biến dự báo và một hoặc nhiều biến độc lập.
Mối quan hệ giữa hai biến này được coi là tuyến tính, tức là, nếu y là biến phụ thuộc và x được coi là biến độc lập, thì mối quan hệ hồi quy tuyến tính của hai biến sẽ giống như phương trình được đề cập dưới đây:
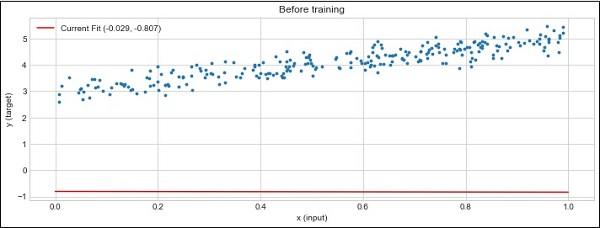
Y = Ax+bTiếp theo, thiết kế một thuật toán cho hồi quy tuyến tính để hiểu hai khái niệm quan trọng được đưa ra dưới đây:
- Cost Function
- Gradient Descent Algorithms
Biểu diễn giản đồ của hồi quy tuyến tính như sau :
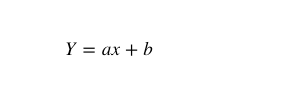
- Giá trị của a là hệ số góc.
- Giá trị của b là giao điểm y.
- r là hệ số tương quan.
- r2 là hệ số tương quan.
Hình ảnh đồ thị của phương trình hồi quy tuyến tính như sau :
Các bước sau được sử dụng để thực hiện hồi quy tuyến tính bằng PyTorch:
Bước 1 :
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import seaborn as sns
import pandas as pd
%matplotlib inline
sns.set_style(style = 'whitegrid')
plt.rcParams["patch.force_edgecolor"] = TrueBước 2
Tạo một tập huấn luyện duy nhất với tập dữ liệu có sẵn
m = 2 # slope
c = 3 # interceptm = 2 # slope
c = 3 # intercept
x = np.random.rand(256)
noise = np.random.randn(256) / 4
y = x * m + c + noise
df = pd.DataFrame()
df['x'] = x
df['y'] = y
sns.lmplot(x ='x', y ='y', data = df)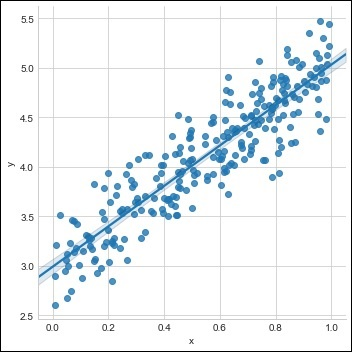
Bước 3
Tiến hành hồi quy tuyến tính với các thư viện PyTorch
import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')
class LinearRegressionModel(nn.Module):
def __init__(self, input_dim, output_dim):
super(LinearRegressionModel, self).__init__()
self.linear = nn.Linear(input_dim, output_dim)
def forward(self, x):
out = self.linear(x)
return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()
def get_param_values():
return w.data[0][0], b.data[0]
def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
plot_current_fit('Before training')Đồ thị kết quả như sau :