1. Biểu thức toán học :
Sử dụng một tập con TeXmarkup trong bất kỳ chuỗi văn bản Matplotlib nào bằng cách đặt nó bên trong một cặp dấu đô la ($).
# math text
plt.title(r'$\alpha > \beta$')Để tạo chỉ số dưới và chỉ số trên, hãy sử dụng các ký hiệu ‘_’ và ‘^’ –
r'$\alpha_i> \beta_i$'
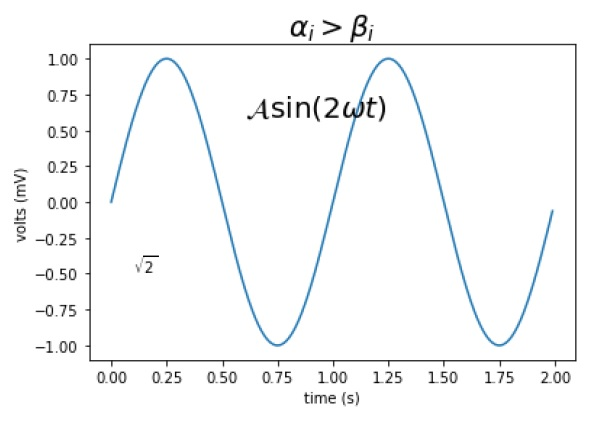
import numpy as np
import matplotlib.pyplot as plt
t = np.arange(0.0, 2.0, 0.01)
s = np.sin(2*np.pi*t)
plt.plot(t,s)
plt.title(r'$\alpha_i> \beta_i$', fontsize=20)
plt.text(0.6, 0.6, r'$\mathcal{A}\mathrm{sin}(2 \omega t)$', fontsize = 20)
plt.text(0.1, -0.5, r'$\sqrt{2}$', fontsize=10)
plt.xlabel('time (s)')
plt.ylabel('volts (mV)')
plt.show()Kết quả :
2. matplotlib.mathtext
mathtext là một mô-đun để phân tích cú pháp một tập hợp con trong toán học TeX và vẽ chúng vào phần mềm phụ trợ matplotlib.
Để biết cách sử dụng nó, hãy xem Viết biểu thức toán học. Tài liệu này chủ yếu liên quan đến chi tiết triển khai.
Mô-đun sử dụng pyparsing để phân tích cú pháp biểu thức TeX.
Bản phân phối Bakoma của phông chữ TeX Computer Modern và phông chữ STIX được hỗ trợ. Có hỗ trợ thử nghiệm cho việc sử dụng các phông chữ tùy ý, nhưng kết quả có thể khác nhau nếu không có sự tinh chỉnh và chỉ số phù hợp cho các phông chữ đó.
3. Ví dụ :
import matplotlib.pyplot as plt
import subprocess
import sys
import re
# Selection of features following "Writing mathematical expressions" tutorial
mathtext_titles = {
0: "Header demo",
1: "Subscripts and superscripts",
2: "Fractions, binomials and stacked numbers",
3: "Radicals",
4: "Fonts",
5: "Accents",
6: "Greek, Hebrew",
7: "Delimiters, functions and Symbols"}
n_lines = len(mathtext_titles)
# Randomly picked examples
mathext_demos = {
0: r"$W^{3\beta}_{\delta_1 \rho_1 \sigma_2} = "
r"U^{3\beta}_{\delta_1 \rho_1} + \frac{1}{8 \pi 2} "
r"\int^{\alpha_2}_{\alpha_2} d \alpha^\prime_2 \left[\frac{ "
r"U^{2\beta}_{\delta_1 \rho_1} - \alpha^\prime_2U^{1\beta}_"
r"{\rho_1 \sigma_2} }{U^{0\beta}_{\rho_1 \sigma_2}}\right]$",
1: r"$\alpha_i > \beta_i,\ "
r"\alpha_{i+1}^j = {\rm sin}(2\pi f_j t_i) e^{-5 t_i/\tau},\ "
r"\ldots$",
2: r"$\frac{3}{4},\ \binom{3}{4},\ \genfrac{}{}{0}{}{3}{4},\ "
r"\left(\frac{5 - \frac{1}{x}}{4}\right),\ \ldots$",
3: r"$\sqrt{2},\ \sqrt[3]{x},\ \ldots$",
4: r"$\mathrm{Roman}\ , \ \mathit{Italic}\ , \ \mathtt{Typewriter} \ "
r"\mathrm{or}\ \mathcal{CALLIGRAPHY}$",
5: r"$\acute a,\ \bar a,\ \breve a,\ \dot a,\ \ddot a, \ \grave a, \ "
r"\hat a,\ \tilde a,\ \vec a,\ \widehat{xyz},\ \widetilde{xyz},\ "
r"\ldots$",
6: r"$\alpha,\ \beta,\ \chi,\ \delta,\ \lambda,\ \mu,\ "
r"\Delta,\ \Gamma,\ \Omega,\ \Phi,\ \Pi,\ \Upsilon,\ \nabla,\ "
r"\aleph,\ \beth,\ \daleth,\ \gimel,\ \ldots$",
7: r"$\coprod,\ \int,\ \oint,\ \prod,\ \sum,\ "
r"\log,\ \sin,\ \approx,\ \oplus,\ \star,\ \varpropto,\ "
r"\infty,\ \partial,\ \Re,\ \leftrightsquigarrow, \ \ldots$"}
def doall():
# Colors used in mpl online documentation.
mpl_blue_rvb = (191. / 255., 209. / 256., 212. / 255.)
mpl_orange_rvb = (202. / 255., 121. / 256., 0. / 255.)
mpl_grey_rvb = (51. / 255., 51. / 255., 51. / 255.)
# Creating figure and axis.
plt.figure(figsize=(6, 7))
plt.axes([0.01, 0.01, 0.98, 0.90], facecolor="white", frameon=True)
plt.gca().set_xlim(0., 1.)
plt.gca().set_ylim(0., 1.)
plt.gca().set_title("Matplotlib's math rendering engine",
color=mpl_grey_rvb, fontsize=14, weight='bold')
plt.gca().set_xticklabels("", visible=False)
plt.gca().set_yticklabels("", visible=False)
# Gap between lines in axes coords
line_axesfrac = (1. / (n_lines))
# Plotting header demonstration formula
full_demo = mathext_demos[0]
plt.annotate(full_demo,
xy=(0.5, 1. - 0.59 * line_axesfrac),
color=mpl_orange_rvb, ha='center', fontsize=20)
# Plotting features demonstration formulae
for i_line in range(1, n_lines):
baseline = 1 - (i_line) * line_axesfrac
baseline_next = baseline - line_axesfrac
title = mathtext_titles[i_line] + ":"
fill_color = ['white', mpl_blue_rvb][i_line % 2]
plt.fill_between([0., 1.], [baseline, baseline],
[baseline_next, baseline_next],
color=fill_color, alpha=0.5)
plt.annotate(title,
xy=(0.07, baseline - 0.3 * line_axesfrac),
color=mpl_grey_rvb, weight='bold')
demo = mathext_demos[i_line]
plt.annotate(demo,
xy=(0.05, baseline - 0.75 * line_axesfrac),
color=mpl_grey_rvb, fontsize=16)
for i in range(n_lines):
s = mathext_demos[i]
print(i, s)
plt.show()
if '--latex' in sys.argv:
# Run: python mathtext_examples.py --latex
# Need amsmath and amssymb packages.
fd = open("mathtext_examples.ltx", "w")
fd.write("\\documentclass{article}\n")
fd.write("\\usepackage{amsmath, amssymb}\n")
fd.write("\\begin{document}\n")
fd.write("\\begin{enumerate}\n")
for i in range(n_lines):
s = mathext_demos[i]
s = re.sub(r"(?<!\\)\$", "$$", s)
fd.write("\\item %s\n" % s)
fd.write("\\end{enumerate}\n")
fd.write("\\end{document}\n")
fd.close()
subprocess.call(["pdflatex", "mathtext_examples.ltx"])
else:
doall()
Kết quả :
0 $W^{3\beta}_{\delta_1 \rho_1 \sigma_2} = U^{3\beta}_{\delta_1 \rho_1} + \frac{1}{8 \pi 2} \int^{\alpha_2}_{\alpha_2} d \alpha^\prime_2 \left[\frac{ U^{2\beta}_{\delta_1 \rho_1} - \alpha^\prime_2U^{1\beta}_{\rho_1 \sigma_2} }{U^{0\beta}_{\rho_1 \sigma_2}}\right]$
1 $\alpha_i > \beta_i,\ \alpha_{i+1}^j = {\rm sin}(2\pi f_j t_i) e^{-5 t_i/\tau},\ \ldots$
2 $\frac{3}{4},\ \binom{3}{4},\ \genfrac{}{}{0}{}{3}{4},\ \left(\frac{5 - \frac{1}{x}}{4}\right),\ \ldots$
3 $\sqrt{2},\ \sqrt[3]{x},\ \ldots$
4 $\mathrm{Roman}\ , \ \mathit{Italic}\ , \ \mathtt{Typewriter} \ \mathrm{or}\ \mathcal{CALLIGRAPHY}$
5 $\acute a,\ \bar a,\ \breve a,\ \dot a,\ \ddot a, \ \grave a, \ \hat a,\ \tilde a,\ \vec a,\ \widehat{xyz},\ \widetilde{xyz},\ \ldots$
6 $\alpha,\ \beta,\ \chi,\ \delta,\ \lambda,\ \mu,\ \Delta,\ \Gamma,\ \Omega,\ \Phi,\ \Pi,\ \Upsilon,\ \nabla,\ \aleph,\ \beth,\ \daleth,\ \gimel,\ \ldots$
7 $\coprod,\ \int,\ \oint,\ \prod,\ \sum,\ \log,\ \sin,\ \approx,\ \oplus,\ \star,\ \varpropto,\ \infty,\ \partial,\ \Re,\ \leftrightsquigarrow, \ \ldots$